Teilprojekt C6
Materialcharakterisierung und numerische Simulation von adaptiven Werkstoffverbunden
Leiter:
Prof. Dr.-Ing. Reinhard Lerch
Friedrich-Alexander-Universität Erlangen-Nürnberg
Lehrstuhl für Sensorik
Paul-Gordan-Str. 3/5
91052 Erlangen
Telefon: 09131 / 85 23131
Telefax: 09131 / 85 23133
E-Mail: reinhard.lerch@lse.eei.uni-erlangen.de
Dr. techn. Stefan Johann Rupitsch
Friedrich-Alexander-Universität Erlangen-Nürnberg
Lehrstuhl für Sensorik
Paul-Gordan-Str. 3/5
91052 Erlangen
Telefon: 09131 / 85 23141
Telefax: 09131 / 85 23133
E-Mail: stefan.rupitsch@lse.eei.uni-erlangen.de
Ansprechpartner:
Dipl.-Ing. Jürgen Ilg
Friedrich-Alexander-Universität Erlangen-Nürnberg
Lehrstuhl für Sensorik
Paul-Gordan-Str. 3/5
91052 Erlangen
Telefon: 09131 / 85 23143
Telefax: 09131 / 85 23133
E-Mail: juergen.ilg@lse.eei.uni-erlangen.de
Motivation
Zielsetzung
Für die Großserienfertigung ist es darüber hinaus von zentraler Bedeutung, für die Materialdaten der Piezokeramik den auftretenden Toleranzbereich (Mittelwert ± Vertrauensgrenzen) und Temperaturabhängigkeiten zu bestimmen. Im Hinblick auf den aktorischen Einsatz der Werkstoffverbunde müssen zudem die nichtlinearen Materialgesetze (Großsignalverhalten, Hysteresephänomene) bei der numerischen Simulation des mechanischen und elektrischen Verhaltens berücksichtigt werden. Hierfür sollen im Rahmen des Teilprojektes unterschiedliche Ausführungen der makroskopischen Hysteresemodellierung untersucht werden.
Methoden
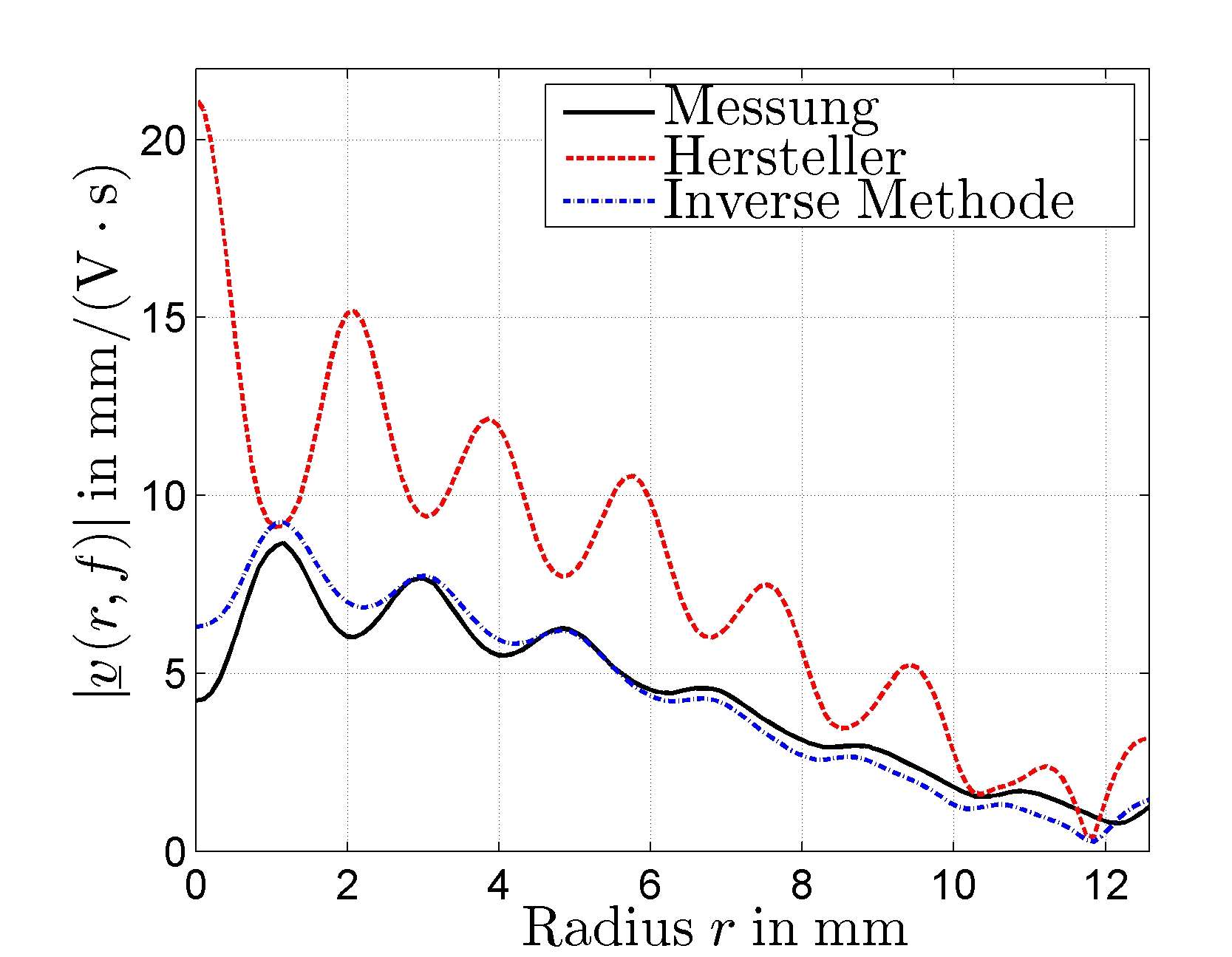 |
Bild 1:
Ortsaufgelöste Normaloberflächengeschwindigkeit für die Dicken-Mode-Schwingung einer Piezo-Scheibe aus Pz27 mit 25mm Durchmesser und 2mm Höhe. Die numerische Simulation erfolgte sowohl mit den Herstellerdaten, als auch mit den mit Hilfe der Inversen Methode ermittelten Daten.
|
Das Inverse Verfahren soll im Hinblick auf die Anwendbarkeit für unterschiedliche Geometrien der Verbunde und Bauformklassen von piezokeramischen Aktoren (scheibenförmige oder quaderförmige Bulk-Keramiken bzw. Piezo-Patches) untersucht werden. In weiterer Folge soll diese Methode auch genutzt werden um Toleranzbereiche und Temperaturabhängigkeiten der Materialparameter zu bestimmen.
Für die Beschreibung des Großsignalverhaltens (Hystereseeigenschaften) soll eine Modellierung mit dem sogenannten Preisach-Hystereseoperator implementiert werden. Dabei wird eine nichtlineare Abbildung zwischen den entsprechenden mechanischen oder elektrischen Größen hergestellt. Diese Identifikation dieser Abbildungen (gewichtete Schaltoperatoren) erfolgt phänomenologisch. Vor allem der, verglichen mit anderem Methoden, geringe Rechenaufwand bei gleichzeitig guten Ergebnissen spricht für diese Vorgehensweise.
|
|
Bild 2a: Preisach-Ebene, α und β sind die Schaltpunkte des Preisach-Hystereseoperators |
||
|
|
Bild 2b: Elektrischer Verschiebungsfluss über elektrischer Feldstärke |
||
|
|
Bild 2c: Dehnung über elektrischer Feldstärke |




